青空ページ meteorology meteoros めておろし
ちょっと寄ってこ。。。「めておろし」
「METEOROLOGY」にちなんで、青空ページの「別名」を「めておろし」と称しています。
この言葉「めておろし」は、肩のこらない話のときに使うこととします。
肩の力を抜いた話は、雨後の「ひどいぬかるみ」状態のようなもので、いたるところで
思い出したように、道路を掘り返しています。
Last Updated : 1997-12/31、1998-1/9,1/21,2000-3/06,2001-12/20,2002-4/14, 2005-10/16
。。。。足元を悪くして、すみません。。。
Return Home
おろし考 :
日本中至る所、「xxおろし」があります。 赤城おろし、鈴鹿おろし、、、
なかでも「六甲おろし」は特定の野球場で猛烈に吹き、ローカルな気象現象として
気象予報士よりもむしろ野球ファンによく知られています。
(関連用語−−−>カタバチック風、フェーン、ボラ)
「大根おろし」とどう言う関係があるのか、真偽のほどは定かではありませんが、
さる大学の文学部で言語学的調査を行ったそうです。 その担当教授曰く、
「いずれ東風が吹き、梅の香が漂ってきたときに、調査結果を公表する」と言うことでしたが
未だその気配がありません。
戻り
だし考 :
山形県清川村の「清川だし」が有名です。清川は最上川が新庄盆地から出羽丘陵を横切って
庄内平野にでようとする所に位置しているために、谷に沿った 収束風 (東風となる)が強く
吹くことがおもな原因である。 このときには、上層に強い南風が吹走しているので、
この東風はこの上層風に伴う摩擦風として発生するものと見られている。
(気象学ハンドブック、P.878ー879より抜粋)。
稲の成育等、農作物に対し甚大な被害(風害)をもたらすことがあるようです。
船出に便利な出風(だしかぜ)の意味、と新版 気象の事典、P.335にあり。
「おろし」とか「だし」とか、今夜のおかず予報は天麩羅、予算によってはなべ物となるでしょう。
戻り
雲をつかむ話 :
 藤原咲平の著作に「雲をつかむ話」と言う昭和初期(1926年即ち。。?)の本が、
復刻版として書店で見受けられますが、よくまあ、このような題名をつけたものですね。
今から70余年前、この作者はこの題名を付けたとき、「ニヤリ」としたに違いない。
この題名を、外国語、たとえば、 A story of grasping clouds等と翻訳すると面白くもなんともない。
言語の頭脳におよぼす力は、「見かけの力」よりも含蓄があって、記憶に残り易いです。
戻り
「見かけの力」って「虚な力」なのでしょうか :
筆者には分りません。
この世の中、「静止している物体の運動を論ずる」ほどヒマではなさそうです。
「物体の運動を論ずる」と言ったとたん、その物体は「動いている」に違いない。
その動いている物体に「見かけの力」が生ずるようです。
何がなんだか、分ったような、分らないような、思考の深みにはまり込みそうな危険性を
秘めている議論になるかも。。。。
戻り
藤原咲平の著作に「雲をつかむ話」と言う昭和初期(1926年即ち。。?)の本が、
復刻版として書店で見受けられますが、よくまあ、このような題名をつけたものですね。
今から70余年前、この作者はこの題名を付けたとき、「ニヤリ」としたに違いない。
この題名を、外国語、たとえば、 A story of grasping clouds等と翻訳すると面白くもなんともない。
言語の頭脳におよぼす力は、「見かけの力」よりも含蓄があって、記憶に残り易いです。
戻り
「見かけの力」って「虚な力」なのでしょうか :
筆者には分りません。
この世の中、「静止している物体の運動を論ずる」ほどヒマではなさそうです。
「物体の運動を論ずる」と言ったとたん、その物体は「動いている」に違いない。
その動いている物体に「見かけの力」が生ずるようです。
何がなんだか、分ったような、分らないような、思考の深みにはまり込みそうな危険性を
秘めている議論になるかも。。。。
戻り
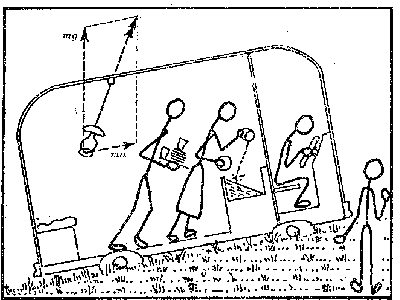
「見かけの鉛直」
と言う今まで聞いたことがなかったような発想とタイトルの、見事な説明を見つけました。
N.F.Barber著「水の波」P.5、 P.8より転載させて頂きます。
「みかけの力」を理解する前準備として、この「みかけの鉛直」の2図を
特に、力の方向(加速度の方向)に注目してジックリ眺めて見て下さい。
(外国の文献には、このような本質を分かりやすく説明しようとする姿勢のある本が見受けられます)
坂道を上るバス内の吊り下げランプの傾き、人々の傾き、水の落下方向に注目(みかけの鉛直を説明する 図1)
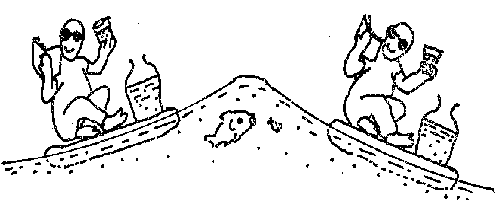
いかだは傾いているが、乗っている人は転落しない。容器の水面にも注目(みかけの鉛直を説明する 図2)
 戻り
戻り
角運動量保存則の話 :
猫は逆さまに落とされても、ちゃんと着地出来る。
フィギュア・スケーターは角運動量保存則を身をもって、実感している。
気象予報士は、角運動量保存則をいかにとらえているのでしょうか。
偏東風、偏西風、大循環を議論するときに登場して来るようです。
地球と大気は角運動量を授受して相互にバランスしているようですが、どうもピンと来ない物理量ですね。
そもそも、角運動量なるものが正体不明である。更に角運動量が保存されて、何がどうなるのかが
具体的に分らない。角運動量保存則を知らなくとも天気の予想はできるでしょうが、でも、筆者の勉強不足です。
いずれヒマが出来たら、勉強しようと思っています。
どうも、理論には眼前の現象を説明する理論と、その背後にある現象を説明する理論の2種類の理論が
ある様な気がします。後者の理論は、あまりにも大きく、それこそ「雲をつかむ」ような話みたいな気がします。
戻り
先達はあらまほしき...の話 :
今から40年以上前、私が中学3年の時買った「徒然草新解」なる受験参考書がいまだ手元にあり、
大事にして、つれづれな時に読み返しています。
「52段」に、「仁和寺にある法師〈予報士にあらず)、年よるまで石清水を拝まざりければ、
心うくおぼえて、或時思ひ立ちて、ただ一人かちより詣でけり。 云々。 少しの事にも
先達はあらまほしき事なり。」と、世の中を知らない頭のかたい法師の面白い失敗談があります。
(何やら、かく言う筆者自身の姿をその法師に見る様な気がしますが)。
天気図を見るのも同様で、先輩、先人の話をよく聞くことは道を間違えないための、大事なことのようです。
過日、天気図検討会なる集まりがあり、テーブルをよせ集めてその上に50枚もある天気図を並べて(壮観!!)
24H,36H,48H,72Hの天気、気温、風、降水量を予想してみる、と言う課題を与えられ、
参加者が3チームに分かれて、札幌、東京、福岡の3地点の予想を行って見ました。
各チームの発表後、その席上その道の達人,厳かに口を開きて曰く:
・みんな、予想のことばかり考える、本当はその前に、もっと現状、過去をじっくり検討しなさい。
・大きな波動を見なさい。
・大局的に、シノプティックに見なさい。いきなり、ローカルなことを考えないこと。
・たとえば-30度に着目し、その-30度の等温線を黄色で塗りその日々の移動の様子を追跡しなさい。
・雲の姿を見なさい。雲がなぜそこに、そのようにあるかが分れば、それで予報は出来るのです。
・700hPaの上昇流域は、ひまわり雲画像の雲域に対応するのだ。
・本日以前の状況の検討を1時間したら、予報は15分で出来ます。
・10年の天気図を頭の中に入れておきなさい。
・電子計算機の結果は信用しなさい。
と。 げに、先達はあらまほしき事なり、と思ひしか。
戻り
天井の露の話 :
寺田寅彦の随筆集を学生のころ良く読みました。
その中で、たしか「茶碗の湯」と言うタイトルで、立ち上る湯気を先生観察して、想像を地球規模の大気の運動に
まで広げて論じていた、かに記憶しています。
話は、少し違いますが、温泉場で「露が天井からポタリと落ちる」のは、水蒸気の凝結の仕組みが
そこにも働いている事になりますね。
その露が天井から一度に、多量に落ちて来れば、きっと湯治客は、「ときならぬ雨が降ってきた」とビックリするでしょう。
自然界には、見えない天井があって、その見えない天井から「露」が落ちてくる仕組みになっているのでしょうか。
(たぶん、凝結核が天井の代わりになっているのでしょう)
戻り
うねりは英国まで ? :
日本付近で発達した台風による「うねり」は英国まで到達するでしょうか。
ついでに、大圏コースの逆ルート〈下図)の「航路」の設定は可能かどうか検討して見て下さい。
地球儀があれば、糸などを使って大陸へのかかり具合を検討してみると面白いですよ。
日本からホーン岬までは、太平洋上を順調に航行できますが、
ホーン岬あたりから以北の大圏コースが、ブラジルの東端やアフリカの西端にかかりそうな気配です。
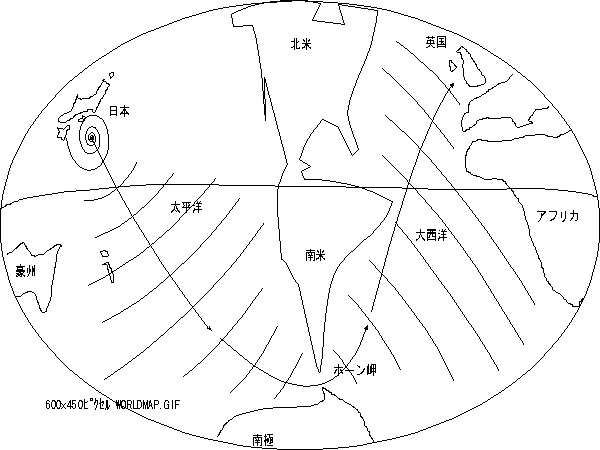 戻り
数式の話
数式、方程式、分子式、構造式など「式」によってある関係を表現することは、自然科学の常套手段です。
換算率、変化率、比例・反比例、定数、つり合い、物理量の保存
等いろいろな関係を表現します。
さて、y=axの時、yはxに比例することは疑いないですが、
ω=2π/86400 のとき、同じ論法を採用できるでしょうか。否です。
外見上、同じ形式をしていても、意味が全く異なりますね。
と、すると私たちは「式が表現しようとしていること」を、いかにして認識出来るでしょうか。
その式に於いて用いられている数字や変数に内在している意味や性質を良く承知しておく必要があります。
気象学には、種々の「式」が登場して来ますが、式は因果関係(自然のストーリー)を記述した台本みたいなもので、
変数や定数は、さしずめストーリーを演ずる「役者」とでも言えましょうか。
「式」を暗記しておくと便利なこともりますが、本来的なストーリーを忘れないようにしなければなりません。
特に近似や微小項の省略の結果導出された式には、要注意です。
「式の成立条件」を逸脱しての議論は誤った結果に到達する恐れがありますので。
地衡風の風速を求める時の式 : fv=1/ρ・Δp/L は、単位unitは加速度を表しますが、
加速度の釣り合いでは意味が通りません。 実感出来る、重量を加味すると、式に意味が見えてきます。
この項、面白くもなんともありません、ハイ。
ただ言いたかった事は、青い字の箇所のような事を発見・認識することが「科学の心」に通ずるのかなあ、
と思った次第です。
戻り
気圧のパラドックス
底面積1平方mの立方体の容器に300K,1気圧の大気を封入する。
立方体内外の空気の出入りはないものとする。
今、容器の温度を30℃低下したとする。
気体の状態方程式 P=ρRT より、容器内の圧力はおよそ0.9気圧となる。
一方、容器内の大気の重量は不変であるから、底面にかかる重量は、温度変化にかかわらず
変わらないはずである。従って気圧は低下しないはずだが、何故低下したのか。
皆さん、考えて見てください、
ヒント: P=ρRT と ΔP=ρgΔZ の2式を成立させる条件、
2式が成立する条件の相違をクリヤーにして下さい。
これらの式が、本質的に、なにを表現しようとしているのかを思い出して下さい。
戻り
戻り
数式の話
数式、方程式、分子式、構造式など「式」によってある関係を表現することは、自然科学の常套手段です。
換算率、変化率、比例・反比例、定数、つり合い、物理量の保存
等いろいろな関係を表現します。
さて、y=axの時、yはxに比例することは疑いないですが、
ω=2π/86400 のとき、同じ論法を採用できるでしょうか。否です。
外見上、同じ形式をしていても、意味が全く異なりますね。
と、すると私たちは「式が表現しようとしていること」を、いかにして認識出来るでしょうか。
その式に於いて用いられている数字や変数に内在している意味や性質を良く承知しておく必要があります。
気象学には、種々の「式」が登場して来ますが、式は因果関係(自然のストーリー)を記述した台本みたいなもので、
変数や定数は、さしずめストーリーを演ずる「役者」とでも言えましょうか。
「式」を暗記しておくと便利なこともりますが、本来的なストーリーを忘れないようにしなければなりません。
特に近似や微小項の省略の結果導出された式には、要注意です。
「式の成立条件」を逸脱しての議論は誤った結果に到達する恐れがありますので。
地衡風の風速を求める時の式 : fv=1/ρ・Δp/L は、単位unitは加速度を表しますが、
加速度の釣り合いでは意味が通りません。 実感出来る、重量を加味すると、式に意味が見えてきます。
この項、面白くもなんともありません、ハイ。
ただ言いたかった事は、青い字の箇所のような事を発見・認識することが「科学の心」に通ずるのかなあ、
と思った次第です。
戻り
気圧のパラドックス
底面積1平方mの立方体の容器に300K,1気圧の大気を封入する。
立方体内外の空気の出入りはないものとする。
今、容器の温度を30℃低下したとする。
気体の状態方程式 P=ρRT より、容器内の圧力はおよそ0.9気圧となる。
一方、容器内の大気の重量は不変であるから、底面にかかる重量は、温度変化にかかわらず
変わらないはずである。従って気圧は低下しないはずだが、何故低下したのか。
皆さん、考えて見てください、
ヒント: P=ρRT と ΔP=ρgΔZ の2式を成立させる条件、
2式が成立する条件の相違をクリヤーにして下さい。
これらの式が、本質的に、なにを表現しようとしているのかを思い出して下さい。
戻り
青い夕焼け
戻り
1997.8.28日付けの「朝日新聞」の報ずる所によれば、
火星の夕焼けは「青い」のだそうです。
火星探査機マーズパスファインダーの撮影した「青い夕焼け」の
写真がNASAからの報道として伝えています。
大気の色が青や赤などになるのは、電磁波が大気粒子により
散乱・吸収される程度によって、呈する色が異なることによる
のでしょうか。
地球の青空は「レーリー散乱」によるものでしたっけ?
なお、気象の事典によれば、レーリー散乱は、
「半径が散乱光の波長の1/10以下の微小球形粒子による光の散乱。」
とあります。
戻り
航走沈下の話
1997.07.02の 東京湾タンカー座礁事故の原因について:
07月21日付けの「朝日新聞」の報ずるところによれば、
『船を海底に引きずり込む「航走沈下」により1メートル沈む?』
ということの様です。
これは、「船体が深く沈む大型船が浅い水域を航行すると、
船底と海底との間隔が狭くなり、その間にはさまれた海水の流速が
速まる」ということで、ベルヌーイの定理により説明できるとの
専門家のコンメントがあります。
『ベルヌーイの定理』とは:
「飛行機が上昇できること」、「野球のボールがカーブすること」、
「テニスでトップ・スピンの球は普通よりも早く落下すること」
等の日常的な例があげられます。
木村 龍治著「流れの科学」P.32〜36の「圧力体験」の中に
平易な説明がありますので参考にしてください。
ここでは、キー・ポイントのみ抜粋引用させて頂きます。
『・圧力差がものを押す力となる(圧力勾配という)
・エネルギー保存則が成立している
( 1/2・ρVの2乗 + ρgH + P = 一定 )』
上式より海水の速度Vが大きくなれば、その海水の圧力Pは
小さくなり、従って船体上部にかかる大気圧との差が大きくなる。
これにより船体は重力方向に押される(すなわち、沈降する)。
追記)エネルギー保存則は、気象の世界では、有効位置エネルギーが
運動エネルギーに変化して、下降流の風速が強まることの説明に
使われていることを思い出して下さい。
追記)それでは、回転しながら進行する低気圧の渦巻は進行が曲げられる
のでしょうか?
低気圧の上方は発散により逆回転となるため、全体として
回転力は受けないこととなる!
(コリオリの見かけの力を考えるべき)
<<===これでよいか、どなたか教えて下さい。
追記)回転するボールが何故まがるか?
今、右回転しながら進行するボールを考えます:
ボールの円周上の(回転軸をとおり)進行方向に直角な方向の
相対する2点を考えます。円周方向の速度をVとするとき、
ボールの進行方向の右側の大気の速度は:
( 進行速度−回転円周速度V )
ボールの進行方向の左側の大気の速度は:
( 進行速度+回転円周速度V )
となり、円周速度Vの2倍分の速度差が生じます。
これが、大気の圧力差すなわち押す力となり、ボールが曲がります。
戻り
当ページに対するご意見、ご質問、ご要望は:
Eメールにてお寄せ下さるようお願い致します。
E−Mail宛先:佐藤 元 satoh@ny.airnet.ne,jp
AZURE 青空
 藤原咲平の著作に「雲をつかむ話」と言う昭和初期(1926年即ち。。?)の本が、
復刻版として書店で見受けられますが、よくまあ、このような題名をつけたものですね。
今から70余年前、この作者はこの題名を付けたとき、「ニヤリ」としたに違いない。
この題名を、外国語、たとえば、 A story of grasping clouds等と翻訳すると面白くもなんともない。
言語の頭脳におよぼす力は、「見かけの力」よりも含蓄があって、記憶に残り易いです。
戻り
「見かけの力」って「虚な力」なのでしょうか :
筆者には分りません。
この世の中、「静止している物体の運動を論ずる」ほどヒマではなさそうです。
「物体の運動を論ずる」と言ったとたん、その物体は「動いている」に違いない。
その動いている物体に「見かけの力」が生ずるようです。
何がなんだか、分ったような、分らないような、思考の深みにはまり込みそうな危険性を
秘めている議論になるかも。。。。
戻り
藤原咲平の著作に「雲をつかむ話」と言う昭和初期(1926年即ち。。?)の本が、
復刻版として書店で見受けられますが、よくまあ、このような題名をつけたものですね。
今から70余年前、この作者はこの題名を付けたとき、「ニヤリ」としたに違いない。
この題名を、外国語、たとえば、 A story of grasping clouds等と翻訳すると面白くもなんともない。
言語の頭脳におよぼす力は、「見かけの力」よりも含蓄があって、記憶に残り易いです。
戻り
「見かけの力」って「虚な力」なのでしょうか :
筆者には分りません。
この世の中、「静止している物体の運動を論ずる」ほどヒマではなさそうです。
「物体の運動を論ずる」と言ったとたん、その物体は「動いている」に違いない。
その動いている物体に「見かけの力」が生ずるようです。
何がなんだか、分ったような、分らないような、思考の深みにはまり込みそうな危険性を
秘めている議論になるかも。。。。
戻り

 戻り
戻り
 戻り
数式の話
数式、方程式、分子式、構造式など「式」によってある関係を表現することは、自然科学の常套手段です。
換算率、変化率、比例・反比例、定数、つり合い、物理量の保存
等いろいろな関係を表現します。
さて、y=axの時、yはxに比例することは疑いないですが、
ω=2π/86400 のとき、同じ論法を採用できるでしょうか。否です。
外見上、同じ形式をしていても、意味が全く異なりますね。
と、すると私たちは「式が表現しようとしていること」を、いかにして認識出来るでしょうか。
その式に於いて用いられている数字や変数に内在している意味や性質を良く承知しておく必要があります。
気象学には、種々の「式」が登場して来ますが、式は因果関係(自然のストーリー)を記述した台本みたいなもので、
変数や定数は、さしずめストーリーを演ずる「役者」とでも言えましょうか。
「式」を暗記しておくと便利なこともりますが、本来的なストーリーを忘れないようにしなければなりません。
特に近似や微小項の省略の結果導出された式には、要注意です。
「式の成立条件」を逸脱しての議論は誤った結果に到達する恐れがありますので。
地衡風の風速を求める時の式 : fv=1/ρ・Δp/L は、単位unitは加速度を表しますが、
加速度の釣り合いでは意味が通りません。 実感出来る、重量を加味すると、式に意味が見えてきます。
この項、面白くもなんともありません、ハイ。
ただ言いたかった事は、青い字の箇所のような事を発見・認識することが「科学の心」に通ずるのかなあ、
と思った次第です。
戻り
気圧のパラドックス
底面積1平方mの立方体の容器に300K,1気圧の大気を封入する。
立方体内外の空気の出入りはないものとする。
今、容器の温度を30℃低下したとする。
気体の状態方程式 P=ρRT より、容器内の圧力はおよそ0.9気圧となる。
一方、容器内の大気の重量は不変であるから、底面にかかる重量は、温度変化にかかわらず
変わらないはずである。従って気圧は低下しないはずだが、何故低下したのか。
皆さん、考えて見てください、
ヒント: P=ρRT と ΔP=ρgΔZ の2式を成立させる条件、
2式が成立する条件の相違をクリヤーにして下さい。
これらの式が、本質的に、なにを表現しようとしているのかを思い出して下さい。
戻り
戻り
数式の話
数式、方程式、分子式、構造式など「式」によってある関係を表現することは、自然科学の常套手段です。
換算率、変化率、比例・反比例、定数、つり合い、物理量の保存
等いろいろな関係を表現します。
さて、y=axの時、yはxに比例することは疑いないですが、
ω=2π/86400 のとき、同じ論法を採用できるでしょうか。否です。
外見上、同じ形式をしていても、意味が全く異なりますね。
と、すると私たちは「式が表現しようとしていること」を、いかにして認識出来るでしょうか。
その式に於いて用いられている数字や変数に内在している意味や性質を良く承知しておく必要があります。
気象学には、種々の「式」が登場して来ますが、式は因果関係(自然のストーリー)を記述した台本みたいなもので、
変数や定数は、さしずめストーリーを演ずる「役者」とでも言えましょうか。
「式」を暗記しておくと便利なこともりますが、本来的なストーリーを忘れないようにしなければなりません。
特に近似や微小項の省略の結果導出された式には、要注意です。
「式の成立条件」を逸脱しての議論は誤った結果に到達する恐れがありますので。
地衡風の風速を求める時の式 : fv=1/ρ・Δp/L は、単位unitは加速度を表しますが、
加速度の釣り合いでは意味が通りません。 実感出来る、重量を加味すると、式に意味が見えてきます。
この項、面白くもなんともありません、ハイ。
ただ言いたかった事は、青い字の箇所のような事を発見・認識することが「科学の心」に通ずるのかなあ、
と思った次第です。
戻り
気圧のパラドックス
底面積1平方mの立方体の容器に300K,1気圧の大気を封入する。
立方体内外の空気の出入りはないものとする。
今、容器の温度を30℃低下したとする。
気体の状態方程式 P=ρRT より、容器内の圧力はおよそ0.9気圧となる。
一方、容器内の大気の重量は不変であるから、底面にかかる重量は、温度変化にかかわらず
変わらないはずである。従って気圧は低下しないはずだが、何故低下したのか。
皆さん、考えて見てください、
ヒント: P=ρRT と ΔP=ρgΔZ の2式を成立させる条件、
2式が成立する条件の相違をクリヤーにして下さい。
これらの式が、本質的に、なにを表現しようとしているのかを思い出して下さい。
戻り