Ｚ軸周りの回転を考えます。

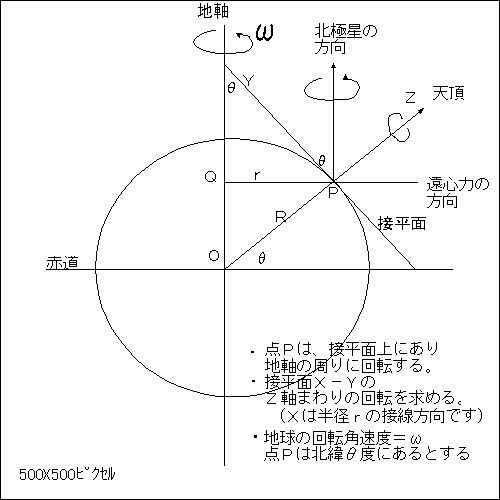北緯 0＜θ＜90度の地点における接平面の回転を求める。

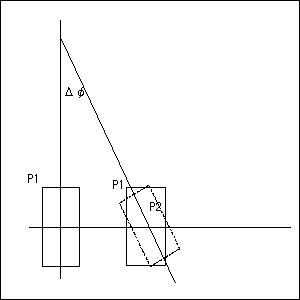地球が微小角Δφだけ回転したとき、接平面Ｐ１がどのように動いて見えるかを考える。

地球外からの観測者には、Ｐ１は動いていないように見える。一方、地球上に固定されたの観測者には　　　　Ｐ１－－＞Ｐ２へ動いているように見える。　　　これは、接平面が移動しようとするとき、慣性により　　　もとの位置にわずかだけ戻ろうとするためである。　このわずかな戻りの積分値がP1-->P2の動きとなって見える。

もちろん、P1上の観測者には自分が動いていることは分らない。しかし、ﾌｰｺｰ振子を見て何かが回転したと思うに違いない。

注意！！! 接平面は、円周方向に地球とともに動く。この動きは、勘定にいれないのである。Ｚ軸周りの回転の有無を見て動く/動かぬと言うのです。どうも紛らわしい!！！

しかも、観測者は地球上接平面上地球外の３人用意しないと説明がしにくいようだ。この接平面は、地球に糊ずけされているのではなくＺ軸まわりに自由に動けるようになっている、と考えること。

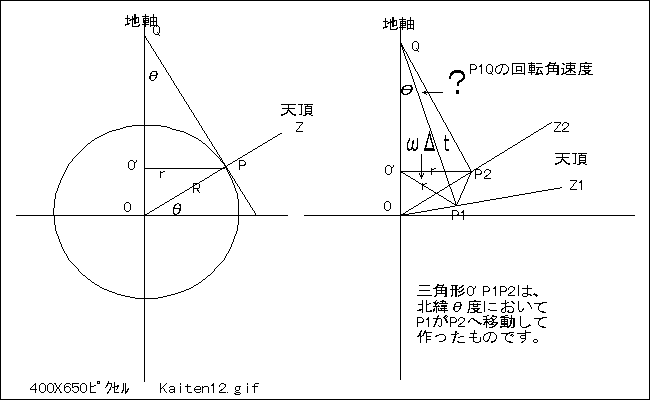
北緯θ度において、Ｏ’Ｐが微小時間Δｔ経過後、ωΔｔだけ回転し、微小三角形Ｏ’Ｐ１Ｐ２を作る。
       Ｏ’Ｐ＝ｒ＝Ｒｃｏｓθ　．．．．．．（１）
　　　Ｐ１Ｐ２＝ωΔｔ・Ｏ’Ｐ
　　　　　　　＝Ｒｃｏｓθ・ωΔｔ．．．．（２）
　　　ＰＱ＝（１／ｔａｎθ）ＰＯ
　　　　　＝（１／ｔａｎθ）Ｒ．．．．．．（３）
　　　Ｐ１Ｐ２＝ＱＰ１・？・Δｔ
　　　　　　　＝ＰＱ・？・Δｔ．．．．．．（４）

（２），（４）のＰ１Ｐ２を等置して、
　　　Ｐ１Ｐ２＝Ｒｃｏｓθ・ωΔｔ
　　　　　　　＝ＰＱ・？・Δｔ．．．．．．（５）　

（５）のＰＱへ、（３）を代入して、
　　　Ｒｃｏｓθ・ωΔｔ＝（１／ｔａｎθ）Ｒ・？・Δｔ．．．．（６）
（６）のＲとΔｔは両辺にあるので、消去して、
　　　ｃｏｓθ・ω＝（１／ｔａｎθ）・？

故に，？＝ｃｏｓθ・ｔａｎθ・ω

　　　　＝　ω・ｓｉｎθ．．．．．．．．．（７）

これは、北緯θ度においける円錐の回転角速度です。

θ＝０度、θ＝９０度において、（７）式が一般的に成立するか否かを検証する。
θ＝９０度において、？＝ωとなり成立。
θ＝０度において、？＝０となり成立。

よって、（７）式は、すべての角度において成立する。

 上述の数式により、北緯θ度における接平面すなわちX-Y平面の回転角速度が求められたことになる。
この角速度は、この平面上で運動する物体に加速度を生じることとなります。
この角速度が、見かけの力を生じることとなります。

QuickLink