フラクタル画像一覧表  
Goto Top page　マンデルブロー博士講演　EXCELで作ったフラクタル画像　Last Updated ;　2002-7/05,7/06,10/31
Accessed :  Since 2002-7/05


#
関数
 Domain
Ｒ，Ｉ
判定条件
初期値
(x0,y0)
複素定数
(A,B)
Cacl.
画像



01
f=z2+C
 Mandel2dim 
-2.0〜0.5,
±1.2
 x2+y2>4
 (0,0)
 A=f1(R,I)
B=f2(R,I)
 50 






02
f=z3+C
 Mandel3dim 
±2,±2
 x2+y2>4
 (0,0)
 A=f1(R,I)
B=f2(R,I)
 50 






03
f=z4+C
 Mandel4dim 
±2,±2
 x2+y2>4
 (0,0)
 A=f1(R,I)
B=f2(R,I)
 50 







04
f=z2+C
Julia2dim
±1.5,±1.5
 x2+y2>4
x0=f1(R,I)
y0=f2(R,I)
 A=-0.3,
B=-0.63
 200 
  





05
f=z3+C
Julia3dim
±1.5,±1.5
 x2+y2>4
 x0=f1(R,I)
y0=f2(R,I)
 A=0.2,
B=1.1
 100 
  





06
f=z4+C
Julia4dim
±2,±2
 x2+y2>4
 x0=f1(R,I)
y0=f2(R,I)
 A=-0.3,
B=-0.63
 100 
  





07
f=z(z+C)/(1+C~z)
Blaschke00
±5,±5
 x2+y2>10
他１点
 x0=f1(R,I)
y0=f2(R,I)
 A=0.82,
B=0.00005
 100 






08
f=z(Z+C/(1+C~z)
Blaschke01
少々時間を要す
±10,±10
 x2+y2>10
他１点
 x0=0.00001,
y0=-0.0005
 A=f1(R,I)
B=f2(R,I)
 50 






09
f=z3-3pz+C
Milnor00
p=-0.5
±1.5,±1.5
 x2+y2>9
他２点
 x0=f1(R,I)
y0=f2(R,I)
 A=0.222,
B=0.124
 100 
 





10
f=λsin(z)
Sine 
±8,±8
 abs(xn)>10
abs(yn)>10
 x0=f1(R,I)
y0=f2(R,I)
 A=-1.0,
B=0.0
 40 
 





11
f=z2+C; Mandel
Julia集合Search用
±2.0,±2.0
 x2+y2>4
 (0,0)
 A=f1(R,I)
B=f2(R,I)
 50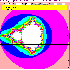 







z=x+yi; C=A+Bi; Domain=(R=rs〜re,I=is〜ie) ← rやiは実部・虚部を、sやeは起点・終点を表す。
Screen=widthxheight=720x720; ｆ1(R,I)=rs+xx(re-rs)/width, f2(R,I)=is+yy(ie-is)/height; 

xx,yy はscreen上の座標(0〜720)。上表で、複素定数(A,B)に数値が入っている図形は、(A,B)を任意に

キーインし変更可能で、様々な図形が描かれます。# 欄Clickで右端の画像を表示・操作可能です。

http://www.ny.airnet.ne.jp/satoh/fractals.htm  All rights reserved. Hajime Satoh 2002