Fractals  
Return home Last Updated: 2002-7/05,7/06,10/31  Accessed:  Since 2002-7/05

Refer to this Japanese version for #5 thru #10, so far


#
Function
 Domain
R, I
Judge Cond.
Initial
(x0,y0)
Complex
(A,B)
Loop
Figure



01
f=z2+C
 Mandel2dim 
-2.0�`0.5,
�}1.2
 x2+y2>4
 (0,0)
 A=f1(R,I)
B=f2(R,I)
 50 






02
f=z3+C
 Mandel3dim 
+-2,+-2
 x2+y2>4
 (0,0)
 A=f1(R,I)
B=f2(R,I)
 50 






03
f=z4+C
 Mandel4dim 
+-2,+-2
 x2+y2>4
 (0,0)
 A=f1(R,I)
B=f2(R,I)
 50 







04
f=z2+C
Julia2dim
+-1.5,+-1.5
 x2+y2>4
x0=f1(R,I)
y0=f2(R,I)
 A=-0.3,
B=-0.63
 200 
  





05
f=z3+C
Julia3dim
+-1.5,+-1.5
 x2+y2>4
 x0=f1(R,I)
y0=f2(R,I)
 A=0.2,
B=1.1
 100 
  





06
f=z4+C
Julia4dim
+-2,+-2
 x2+y2>4
 x0=f1(R,I)
y0=f2(R,I)
 A=-0.3,
B=-0.63
 100 
  





07
f=z(z+C)/(1+C~z)
Blaschke00
+-5,+-5
 x2+y2>10
etc.
 x0=f1(R,I)
y0=f2(R,I)
 A=0.82,
B=0.00005
 100 






08
f=z(Z+C/(1+C~z)
Blaschke01
wait
+-10,+-10
 x2+y2>10
etc.
 x0=0.00001,
y0=-0.0005
 A=f1(R,I)
B=f2(R,I)
 50 






09
f=z3-3pz+C
Milnor00
p=-0.5
+-1.5,+-1.5
 x2+y2>9
etc.
 x0=f1(R,I)
y0=f2(R,I)
 A=0.222,
B=0.124
 100 
 





10
f=Lamda*sin(z)
Sine 
+-8,+-8
 abs(xn)>10
abs(yn)>10
 x0=f1(R,I)
y0=f2(R,I)
 A=-1.0,
B=0.0
 40 
 





11
f=z2+C; Mandel
for Julia 
set Search
+-2.0,+-2.0
 x2+y2>4
 (0,0)
 A=f1(R,I)
B=f2(R,I)
 50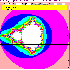 







z=x+yi; C=A+Bi; Domain=(R=rs---re,I=is---ie) --- r,i= real & imaginary number,s,e= start, end.
Screen=widthxheight=720x720; ��1(R,I)=rs+xx(re-rs)/width, f2(R,I)=is+yy(ie-is)/height; 

xx,yy =screen coordinates(0�`720).
Complex number(A,B): substitute A,B with appropriate number.

All rights reserved. Hajime Satoh 2002