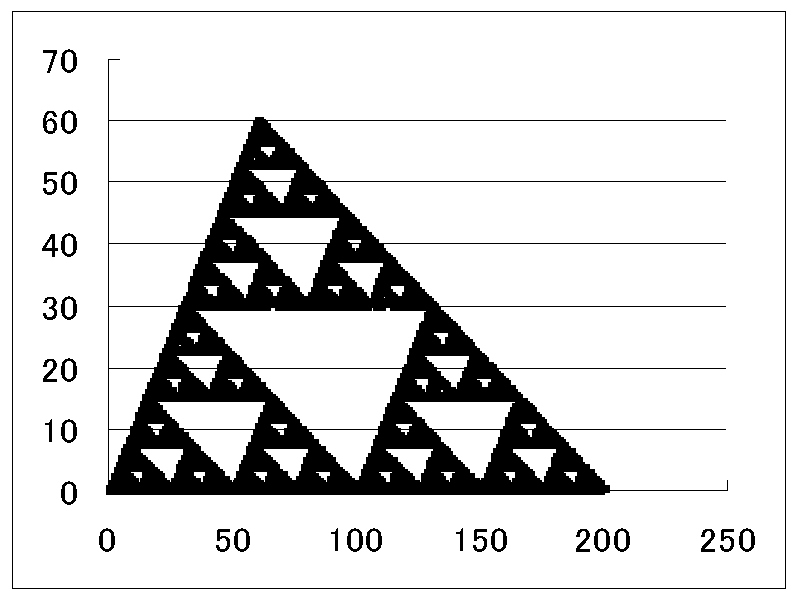
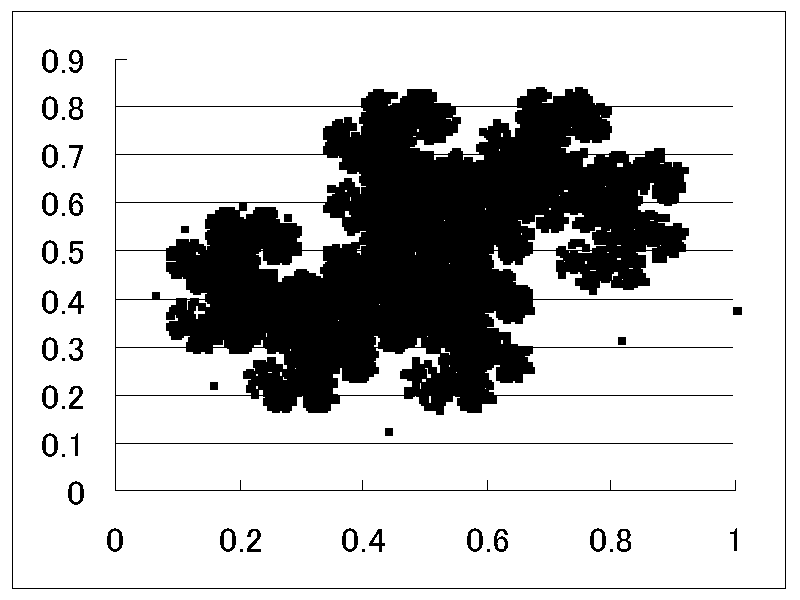
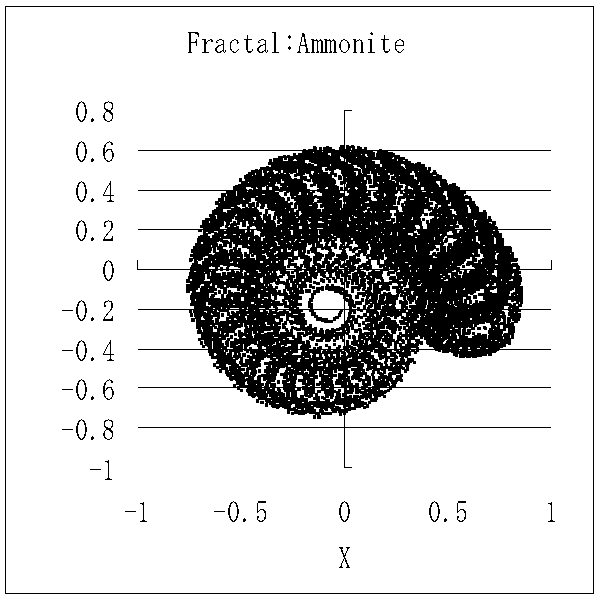
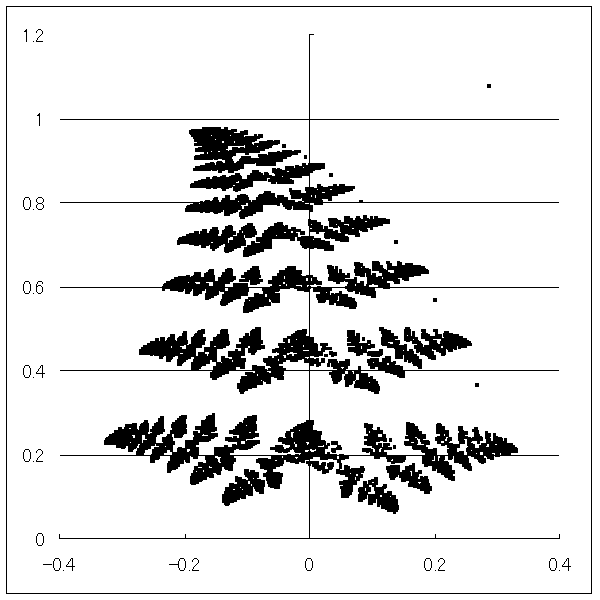
1.ロジスティック波形★ 軌道を動画表示します。
ロジスティック波形 Xn+1=aXn*(1−Xn)が基礎式です。 ロジスティック関数は(Sigmoid関数とかS字関数と言われます)、気象においては、 ニューラルネットワーク(NRN)の情報処理素子としても使われています。 NRNの文献はこちら または、 拙著、「天気図と気象理論」P.131を参照して下さい。 初期値やパラメータをわずかずつ変えて見ると、様々な図形が得られます。 クリックすると計算値や諸条件および画像が表示されます。 Logistic:lg0p9 収束 Logistic:lg2p9 振動&収束 Logistic:lg3p449 周期振動 Logistic:lg3p55 周期振動 Logistic:lg3p831874055 周期振動 Logistic:lg4 カオス Logistic:lg4p001 カオス&計算不能
2.エノン写像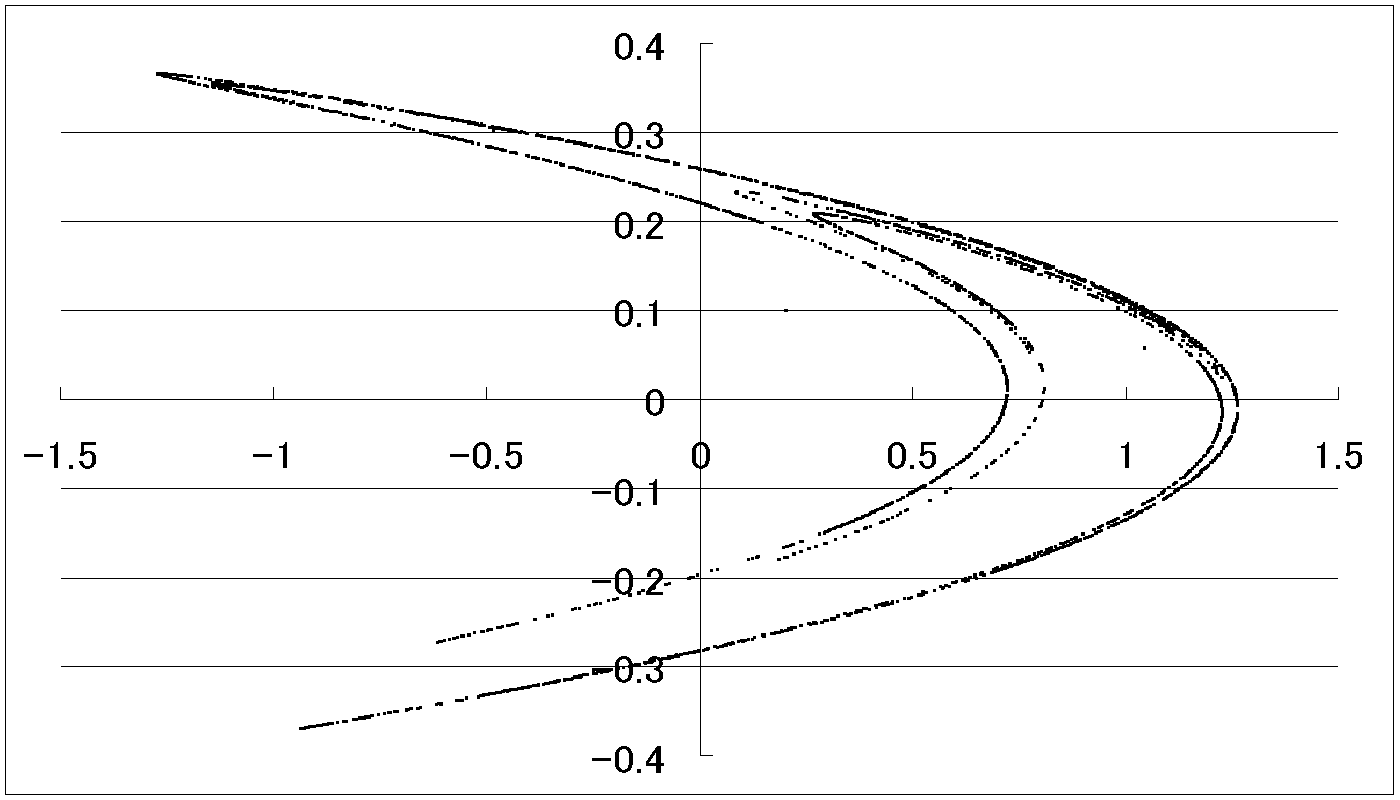
エノン写像 Xn+1=1-aXn*Xn+Yn Yn+1=bXn Henon:hn1p42 エノンの写像 ★ 点を順次プロットしていきます。 プロットをN=12000程度までに増大して見ました。 Henon:hn1p42 エノンの写像(拡大図) nを更に増大すると、もっと細かいところまで見ることができるでしょう。 N=64000にしてみました。 Henon:hn1p42 エノンの写像(拡大図) 数式を少し変形したものです。 Henon:hn2p エノンの写像(バリエーション1) ★ 点を順次プロットしていきます。 変形した数式のパラメータを変えて見ました。 Henon:hn0p49 エノンの写像(バリエーション2) 変形した数式のパラメータを変えて見ました。 Henon:hn0p49 エノンの写像(バリエーション2拡大図) Henon:hn0p49 エノンの写像(バリエーション3) パラメータaを連続的に変えて見ました。 Henon:hn1p05vari エノンの写像(a−Xに関する周期倍化図付き)
3.周期倍加分岐図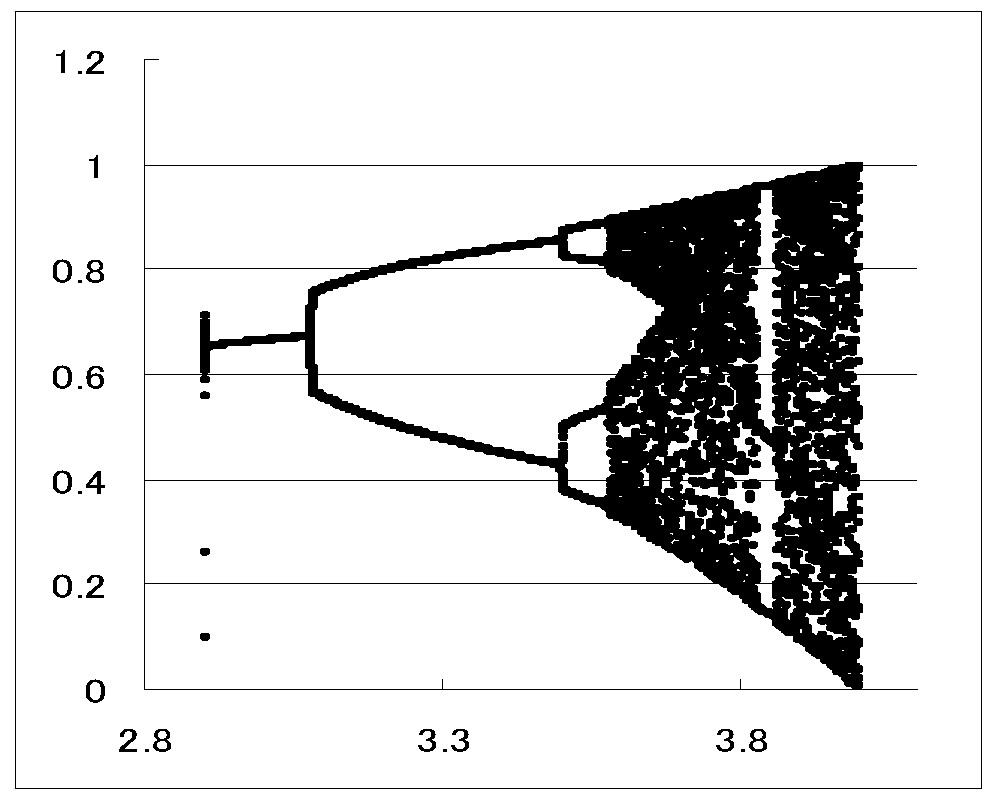
周期倍加分岐図
Xn+1=Xn+a;
Yn+1=Xn*Yn*(1-Yn)
周期倍加
周期倍加(拡大図)
現象は、周期倍分岐する:
ロジスティック写像の周期倍分岐(a−Xに関する周期倍化図付き)
エノンの写像の周期倍分岐(a−Xに関する周期倍化図付き)
4.ローレンツ★ 沸騰:軌道を動画表示します。 ★ 対流:軌道を動画表示します。 ★ 伝導:軌道を動画表示します。 ★ 初期値鋭敏性・誤差の増大の検討 μを順次変えていった場合の形の変化
ローレンツ(「天気図と気象理論」P.127 に記載あります。) ローレンツモデルは下式で与えられます。 ローレンツがNavier-Stokesの公式をベースとして、対流現象を モデル化した数式です: ∂x/∂t=−γx+γy ∂y/∂t=−xz+μx−y ∂z/∂t=xy−bz 上の微分方程式は、コンピューターで計算できませんので、 Xn+1=Xn+(−γXn+γYn)Δt Yn+1=Yn+(−XnZn+μXn−Yn)Δt Zn+1=Zn+(XnYn−bZn)Δt の差分の形式に変形します。 方程式のμを順次変えた場合の、X−Z,X−Yの軌道を示します。 n=1000までの計算結果です。 Lorenz:lzμ84p7 ローレンツ Lorenz:lzμ84p6 ローレンツ Lorenz:lzμ71 ローレンツ Lorenz:lzμ49p8 ローレンツ Lorenz:lzμ28 ローレンツ Java-Codingでの図形(点) Lorenz:lzμ18 ローレンツ Lorenz:lzμ15p0351 ローレンツ Lorenz:lzμ10 ローレンツ Lorenz:lzμ7 ローレンツ Lorenz:lzμ4 ローレンツ Lorenz:lzμ0 ローレンツ Lorenz:lzμm28 ローレンツ Lorenz:lzμm92 ローレンツ Lorenz:lzμm92p59 ローレンツ その他: 変形した式: Xn+1=aXn-Xn*Yn Yn+1=b*Yn+Xn*Xn 与えるパラメーターおよび初期値:(一部の図形には、軌道も描図してあります) Lorenz:lz 渦巻き :a=1.343, b=0.9, c=0, d=0, X0=0.05, Y0=0.05 Lorenz:lz Y軸くっつき :a=1.49, b=0.99, c=0, d=0, X0=0.1, Y0=0 Lorenz:lz 蜘蛛状渦巻き:a=1.501, b=0, c=0, d=0, X0=0.2, Y0=-0.8 Lorenz:lz 顔のヒゲ :a=1.59, b=0.6, c=0, d=0, X0=0.1, Y0=-0.01 Lorenz:lz 対称図形 :a=1.7, b=0.1, c=0, d=0, X0=0.2, Y0=-0.8 Lorenz:lz すかし図 :a=1.88, b=0, c=0, d=0, X0=0.1, Y0=0
5.レスラー
レスラー ローレンツ系は、アトラクターが2つありますが、 レスラー系のアトラクターは、1つです。 分岐パラメーターμを大きくしていくと、軌道は 2重、4重、8重、16重と「周期倍化」していきます。 ∂x/∂t=−Y−Z ∂y/∂t=X+aY ∂z/∂t=b+XZ-μZ 上の微分方程式は、コンピューターで計算できませんので、 Xn+1=Xn−(Yn+Zn)Δt Yn+1=Yn+(Xn+aYn)Δt Zn+1=Zn+(b+XnZn−μZn)Δt の差分の形式に変形します。 (μは、分岐パラメーターと言われます) Rossler:rsab0p2μ3p236 次の図は、周期倍加の筋模様が出ています。 Rossler:rsab0p2μ6p06 Rossler:rsab0p2μ6p06fig(拡大図です) その他の様々なカオスです。 Rossler:rsm6 Rossler:rsm0p1 Rossler:rsab0p2
6.Gumowski & Mira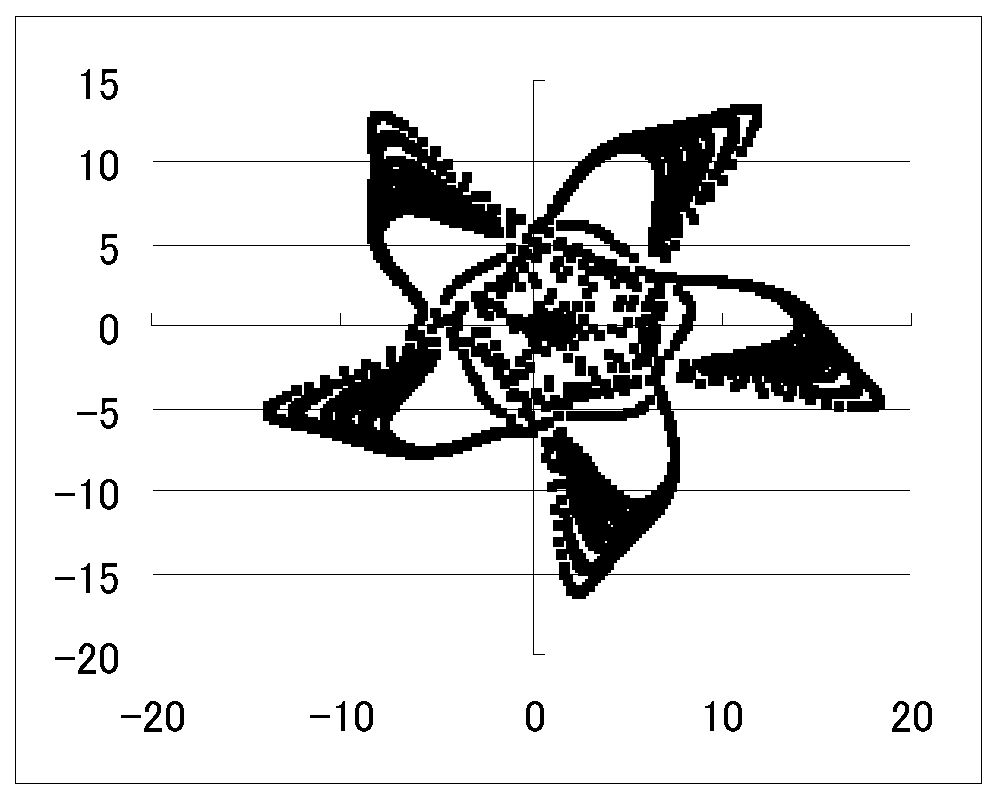
Gumowski & Mira
Xn+1=Yn+a(1−bYn2)Yn+G(Xn)
Yn+1=-Xn+G(Xn+1)
G(Xn)=μXn+(2(1-μ)Xn2)/(1+Xn2)
Gumousuki&Mira:gm 周期倍加関数に似ている
Gumousuki&Mira:gm ヒトデに似ている
Gumousuki&Mira:gm ミジンコに似ている
Gumousuki&Mira:gm 渦巻く4つに似ている
Gumousuki&Mira:gm 渦巻きに似ている
Gumousuki&Mira:gm 渦巻きに似ている
Gumousuki&Mira:gm 円に似ている
Gumousuki&Mira:gm 花火に似ている
Gumousuki&Mira:gm 渦巻き状星雲に似ている
Gumousuki&Mira:gm 羽5枚に似ている
===
追加:
Gumousuki&Mira:gm 卍形に似ている
Gumousuki&Mira:gm 魚のエイに似ている
Gumousuki&Mira:gm 周期倍加のなりかけに似ている
Gumousuki&Mira:gm 7角結晶に似ている
Gumousuki&Mira:gm 渦巻きに似ている
Gumousuki&Mira:gm 星団に似ている
Gumousuki&Mira:gm 丸が10こに似ている
===
変形した式:
Xn+1=aXn+bYn+c+d/(1+Xn*Xn)
Yn+1=-Xn
与えるパラメーターおよび初期値:
Gumousuki&Mira:gm 笹の葉:a=-0.32,b=0.9, c=0, d=15,X0=1, Y0=0
Gumousuki&Mira:gm 羽3枚 :a=-0.9, b=0.96, c=-4,d=5, X0=1, Y0=0
7.Japanese Attractor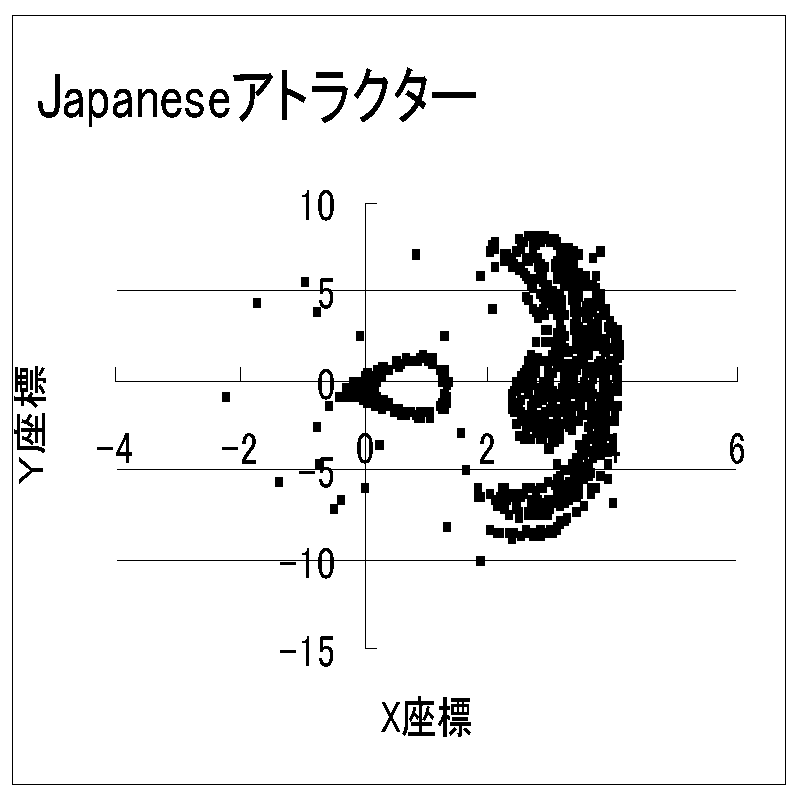
7.ジャパニーズアトラクター
dx/dt=y
dy/dt=-ky-x3+Bcost
この微分方程式を差分の形にします;
Xn+1=Xn+Yn*Δt
Yn+1=Yn+(-k*Yn-Xn*Xn*Xn+B*cost)*Δt
jp:Japanese Attractor
jp:Japanese Attractor(拡大図)