亂摦婡亃 丂丂丂丂仺巻偺忋偵彂偄偰偁傞悢幃傗尰徾傪丄帺暘偺僷僜僐儞偺忋偵嵞尰偟偰 丂丂丂丂丂偝傑偞傑側妏搙偐傜妋偐傔偰傒偨偄丅 丂丂丂丂仺尰徾傪僷僜僐儞偱乽摦偒乿偲偟偰尒傞偙偲偑偱偒丄 丂丂丂丂丂廬偭偰丄尰徾偺乽曄壔乿傪帇妎壔偱偒丄 丂丂丂丂丂尰徾偺乽梊應乿偵娭偟偰偺捈姶揑棟夝傪彆偗傞丅 丂丂曽朄仺婥徾偺棟榑幃傪僾儘僌儔儉壔偟丄帺暘偺僷僜僐儞偱摦偐偡丅 丂丂嵽椏仺嫵壢彂乮堦斒婥徾妛傗抧媴棳懱椡妛摍乯傗婥徾挕摍偺弌斉暔偵宖嵹偝傟偰偄傞 丂丂丂丂丂尰徾傗悢幃傪庡偨傞懳徾偲偟偨丅 丂丂墶揥奐仺僀儞僞乕僱僢僩忋偱傕摦偔傛偆偵偟偨丅
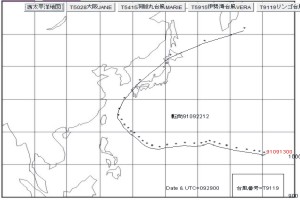
亂尰徾亃晽偵棳偝傟傞戜晽 亂OHP-1丄墌亄倃丒倄幉亃亂OHP-1丄儀僗僩僩儔僢僋亃 丂丂億僀儞僩仺塤傗墝撍偺墝偑晽偵棳偝傟傞丅偱偼丄夞揮偟偰偄傞嬻婥偑巜岦棳偵棳偝 丂丂丂丂丂丂丂傟傞偲偒丄嬻婥夠偺塣摦偺婳愓偼丄偄偐偵側傞偐傪尒傞丅 偦偺慜偵丄 塓偑棳偝傟傞戙昞椺偲偟偰丄戜晽偺儀僗僩僩儔僢僋傪昤偄偰尒傛偆丅 丂丂憖嶌仺巜岦棳偺晽岦丄晽懍傪丄侽丄俁侽丄俆侽m/sec偵曄偊傞丅 丂丂愢柧仺墌廃忋偺堦偮偺嬻婥夠偵拝栚偟丄墌廃忋偺埵抲偵傛偭偰丄昤偔婳愓偑偝傑偞傑 丂丂丂丂丂偲側傞丄偙偲傪尵偆丅
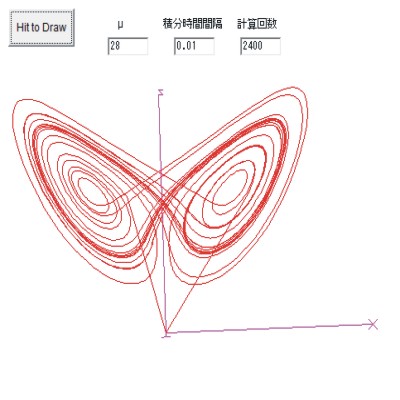
亂悢幃亃晽懍偺梊應丂亂OHP-2丄旝暘曽掱幃亃 丂丂億僀儞僩仺偙偺掱搙偺偙偲偑婥徾偺慺恖偱傕帺戭偱丄帺暘偺僷僜僐儞偱偱偒傞帠椺傪帵偡丅 丂丂憖嶌仺僐儕僆儕椡丄婥埑孹搙椡偺悢抣傪奺庬曄偊偰丄寁嶼偝偣丄晽懍 UV 偺曄壔偺條巕傪昤偔丅 丂丂愢柧仺僾儕儈僥傿僽曽掱幃偺堦晹傪悢抣寁嶼偡傞丅僐儕僆儕椡丄婥埑孹搙椡傪帺桼偵曄偊偰丄 丂丂丂丂丂晽懍偑偄偐偵曄壔偡傞偐傪幚姶偡傞丅 佪倳/佪倲亖亅乮倳佪倳/佪倶亄倴佪倳/佪倷亄倵佪倳/佪倸乯丂 丂 丂丂丂丂 丂亄俀兌倱倝値冇倴亅佪倫/兿佪倶亄俥x丂 丂 佪倴/佪倲亖亅乮倳佪倴/佪倶亄倴佪倴/佪倷亄倵佪倴/佪倸乯丂 丂丂丂丂丂丂丂丂丂丂 丂亅俀兌倱倝値冇倳亅佪倫/兿佪倷亄俥y丂 丂丂娭楢仺僇僆僗偺椺丗儘乕儗儞僣偺僗僩儗儞僕丒傾僩儔僋僞乕傪俁俢夞揮偟偮偮丄徯夘偡傞丅 丂丂丂丂丂佪倶/佪倲=亅兞倶亄兞倷丄丂佪倷/佪倲亖亅倶倸亄兪倶亅倷丄丂佪倸/佪倲亖倶倷亅倐倸
戜晽偺儀僗僩僩儔僢僋 | 僇僆僗乮儘乕儗儞僣偺僗僩儗儞僕丒傾僩儔僋僞乕乯 |